《地统计学》笔记 | myetyet ブログ

概论

地统计学概念
- 定义
  - 地统计学（又称地质统计学）是以区域化变量理论为基础，以变异函数为主要工具，研究在空间分布上既有随机性又有结构性，或空间相关和依赖性的自然现象的科学。
- 具体方面
  - 理论基础：区域化变量理论
  - 主要工具：协方差函数和变异函数
  - 主要内容：克里金插值法
研究内容
- 空间估值
- 局部不确定性预测
- 随机模拟
- 多点地统计学
发展史
- 国外
  - 20世纪50年代前：在其它非地质领域有应用，但没引起注意。
  - 20世纪50年代：D. J. Krige和H. S. Sichel的新矿藏评价方法的提出标志着地统计学雏形的形成。
  - 20世纪60、70年代：1962年法国著名统计学家G. Matheron创立地统计学，地统计学理论和方法的进一步完善和改进。
  - 20世纪70年代末到90年代：大批地统计学研究理论和应用的专著出版。
  - 20世纪90年代之后：地统计学理论、方法及应用发展成熟并拓展，软件出现。
- 国内
  - 起步阶段（1977年至1989年11月）
    - 1977年，地统计学由美国H. M. Parker博士传入我国。
    - 宣传普及、学习研讨、发表论文、有关工业部门和个别矿山企业根据自己的需要，独立进行开发研究，构成了该阶段的主要内容。
  - 第二阶段（1989年11月至1995年10月）
    - 1989年11月召开全国第一届地质统计学学术讨论会，标志着地统计学发展的第二阶段开始。
    - 从开发研究与学术交流活动转向生产实践，与地质勘探和矿山生产相结合。
  - 第三阶段（1995年10月至今）
    - 1995年，地质领域的有关部门公布了“运用地质统计学方法提交地质勘探报告的编写提纲和审查提纲”的试行意见。标志着地统计学技术在我国已经发展成熟，进入深入发展阶段。
应用领域
- 地质学
  - 矿产资源储量计算及平均品位估计
  - 矿产资源预测及找矿勘探
  - 石油勘探开发
- 土壤学
  - 土壤物理性质空间变异
  - 土壤化学性质空间变异
  - 土壤学试验设计和采样方法
  - 土壤质量管理
- 生态学
  - 生态学变量空间变异性的定量描述和解释
  - 生物特征的估计
  - 生态学研究对象的时空变化规律分析
- 环境学
  - 土壤环境研究
  - 水环境研究
  - 其他相关领域研究
- 气象学
相关软件
- ArcGIS地统计模块
- Surfer
- Geo-EAS
- GEOPACK
- Geostatistical Toolbox
- GSLIB
- GS+

地统计学基础

地理要素的数据类型
- 地理数据是用一定的测度标准去描述或衡量地理要素而取得的地理信息。
定量、定性地理数据分类
- 间隔尺度数据：带单位的数据，如千克、摄氏度等。
- 比例尺度数据：规定一个基点，再将其他量换算成与之的比例（没有单位）。
- 有序数据：只表示次序关系的数据，如小雨为、中雨为、大雨为。
- 二元数据：用和表示的数据。
总体和样本
- 总体
  - 定义
    - 根据统计分析或研究目的而确定的同类事物或现象的全体。
  - 理解
    - 总体可以指满足指定条件的元素或个体的集合。
    - 总体的范围根据研究目的而定，并非固定不变。
    - 总体可分为目的总体和抽样总体，并不是固定不变的。
    - 总体可分为定性总体（质量总体）和定量总体（数量总体）。
    - 根据总体包含的元素单位数是否有限，可分为有限总体和无限总体。
- 样本
  - 定义
    - 从总体中抽取若干元素而构成的集合称为样本，也称子样。
  - 理解
    - 目的：从样本特性对总体特性作出统计估计与推断
    - 样本规模：能代表总体的抽样个数
    - 样本分布：均匀、特征点要有分布
- 采样方法
  - 随机抽样
  - 机械抽样（系统采样）
  - 分层抽样
  - 分组抽样
  - 地质统计采样方法
频数分布
- 频数：在相同的条件下进行了次试验，在这次试验中，事件发生的次数称为事件发生的频数。
- 频率：比值称为事件发生的频率，并记为。
- 频数分布表
  - 离散数据频数分布表：直接统计样本值出现的次数和分组做频数分布表。
  - 连续数据频数分布表：确定组数、组距、各组的上下限，然后按样本值大小归组，要求：分组后能够真实的反映总体特征。
  - 累积频率（数）分布表：将各组的频数依次相加就得到累积频数值。
- 频数分布图
  - 直方图：用矩形的宽度和高度来表示频数分布的图形，横轴表示数据分组，纵轴表示频数或频率。
  - 多边形图：在直方图的基础上，把直方图顶部的中点（即组中值）用直线连接起来，再把原来的直方图去掉。
  - 条形图：用宽度相同的条形的高度或长短来表示数据变动的图形，条形图可以横置或纵置。
统计特征数
- 集中性
  - 算数平均数：
  - 中数
  - 众数
- 离散性
  - 极差（全距）
  - 四分位差
  - 离差：
    - 平均离差：
    - 离差平方和：
  - 总体方差：
  - 总体标准差：
  - 变异系数：
- 形态数
  - 偏态数（偏度系数）
    - 定义：对分布偏斜方向和程度的测定
    - 公式：
    - 评价：为负偏态（右偏）；为分布对称；为正偏态（左偏）。
  - 峰态数（峰度系数）
    - 定义：用来反映频数分布曲线顶端尖峭或扁平程度的指标
    - 公式：
    - 评价：为低阔峰；为正态分布；为高狭峰。
相关分析
- 相关关系概念
  - 函数关系：某一个或某几个现象的变动会引起另一个现象确定的变动，它们之间的关系可以用数学函数表示出来。
  - 相关关系：两个或多个现象之间虽然存在某种关系，但这种关系是不确定或不确切的函数关系。
- 相关关系种类
  - 按相关关系的程度分
    - 完全相关
    - 不完全相关
    - 不相关（零相关）
  - 按相关变化方向分
    - 正相关
    - 负相关
  - 按相关形式分
    - 线性相关
    - 非线性相关
  - 按变量数量分
    - 单相关
    - 复相关
    - 偏相关
- 主要内容
  - 确定现象之间有无相关关系以及相关关系的表现形态
  - 确定相关关系的密切程度
- 相关关系测定
  - 相关表
  - 相关图
- 相关程度测定
  - 协方差
    - 公式
      - 定义：
      - 总体：
      - 样本：
    - 特点
      - 可定量的表示两个变量之间的相关程度。
      - 值为正时，为正相关；值为负时，为负相关。
      - 不存在相关关系时，值趋于零或为零。
      - 协方差值受数据值大小的影响。
      - 协方差值是一个有量纲单位的数值。
  - 相关系数
    - 公式
    - 说明
      - 两个变量之间的相关程度和方向取决于两个变量离差乘积之和。
      - 相关程度的大小与计量单位无关，相关系数是无量纲的数量。
      - 相关系数是用来说明变量之间在直线相关条件下相关关系密切程度和方向的统计分析指标，一般只适用于测定变量间的线性相关关系。
      - 若两随机变量相互独立，则协方差和相关系数均为，两者线性不相关；反之若两随机变量线性不相关，则两者不一定线性不相关。
    - 意义
      - ：不存在线性相关关系
      - ：微或无（极低度）线性相关
      - ：低度线性相关
      - ：显著（中度）线性相关
      - ：高度相关
      - ：完全线性正（负）相关
    - 检验步骤
      - 提出原假设和备择假设：假设样本相关系数是抽自具有零相关的总体，即。
      - 查临界值：规定显著性水平，并依据自由度，查分布表确定临界值。
      - 计算检验的统计量：计算。
      - 做出判断：若，则认为两变量线性相关（不线性相关的可能性只有）；反之认为在给定置信水平下两变量不线性相关。
  - 偏相关系数
    - 概念
      - 在多要素所构成的地理系统中，先不考虑其他要素的影响，而单独研究两个要素之间的相互关系的密切程度，这称为偏相关。
      - 用以度量偏相关程度的统计量，称为偏相关系数。
      - 当总共有个变量，固定其中的个，研究剩下的变量时，计算的相关系数称为级相关系数。
    - 说明
      - 只有级偏相关系数才真实地反映了研究的两个相关变量间线性相关的性质与程度。
      - 级偏相关系数共有个。
    - 三个变量的偏相关系数
    - 显著性检验
      - 方法：检验
      - 统计量：
  - 复相关系数
    - 公式
    - 显著性检验
      - 方法：检验
      - 统计量：
    - 与偏相关系数的关系
      - 复相关系数必大于或至少等于单相关系数的绝对值，如。
回归分析
- 概念
  - 回归分析就是对具有高度相关关系的现象，根据其相关的形态，建立一个适宜的数学模型（回归方程），来近似地反映变量之间的一般变化关系，以便于进行估计或预测的统计方法。
- 种类
  - 按涉及自变量的数量分
    - 一元回归分析
    - 多元回归分析
  - 按回归方程的表现形式分
    - 线性回归分析
    - 非线性回归分析
- 主要内容和步骤
  - 确定变量：根据理论和对问题的分析判断，将变量分为自变量和因变量。
  - 建立模型：找出合适的数学方程式（即回归模型）描述变量间的关系。
  - 统计检验：对回归模型进行统计检验。
  - 估计预测：利用回归模型，根据自变量去估计、预测因变量。
- 一元线性回归模型
  - 基本结构
  - 概念
    - 设，其中不依赖于，有，则称为一元线性回归方程。
    - 若记参数、的拟合值分别为（回归常数）、（回归系数），则一元线性经验回归方程（简称回归方程）为，其中为的估计值。
  - 前提条件
    - 两个变量之间确实存在显著的相关关系
    - 两种变量之间确实存在着直线相关关系
  - 参数、的最小二乘估计
    - 记，表示实际观测值与回归值之差。
    - 使。
    - 由于为非负二次函数，其最小值一定存在，同时是、的可微函数，则与应是下面方程组的解：
    - 整理得下面正规方程组：
    - 解得：
    - 同时可以说明经过散点图的几何中心。
  - 显著性检验
    - 方法：检验
    - 相关符号定义
      - 总的离差平方和：
      - 剩余平方和（残差平方和）：
      - 回归平方和：
      - 决定系数（判断系数）：
    - 统计量：
    - 方程显著条件：
- 多元线性回归模型
  - 回归方程
  - 参数的最小二乘估计
    - 使的必要条件为：
    - 整理得下面正规方程组：
    - 引入下面的矩阵：
    - 则有，解得。
  - 显著性检验
    - 方法：检验
    - 统计量：
相关分析与回归分析比较
- 联系
  - 相关分析是回归分析的基础和前提
  - 回归分析是相关分析的继续和深化
- 区别
  - 相关分析中两变量对等，改变两者的地位，并不影响相关系数的数值，只有一个相关系数；回归分析中两变量要确定自变量和因变量，互为因果关系的两个变量可以编制两个独立的回归方程。
  - 相关分析中两变量均为随机变量；回归分析中只有因变量为随机变量。
  - 相关分析测定是否存在相关关系及相关程度和方向；回归分析则是建立回归方程，并用回归模型进行预测和控制。

区域化变量理论

随机场
- 随机变量
  - 定义
    - 设随机实验的样本空间为，若对于，都有一个实数与之对应，且对于任意实数，事件都有确定的概率，则称是一个随机变量。
  - 理解
    - 随机变量本身是一个函数，定义域是样本空间。
    - 随机变量是一实值变量，有一个可能的取值范围，范围随实验不同而不同。
    - 随机变量的取值随实验结果而定，在实验之前不能预知其取什么值。
    - 随机变量的取值具有一定的概率，随机变量是具有一定概率分布的变量。
    - 随机变量和对随机变量的观测，可从总体和抽样的角度来理解。对随机变量每次的观测结果是一个确定的数值，该数值称为随机变量的一个实现。
- 随机函数
  - 定义
    - 设随机实验的样本空间为，对于任一，都有一个函数与之对应（其中），且当各自变量取任意固定值时，函数为一随机变量，则称是定义在上的一个随机函数。
  - 理解
    - 横向：每次随机实验（或观测）的结果都可得到一个确定性的函数，称为随机函数的一个实现，因此随机函数可理解为它的所有实现的集合。
    - 纵向：随机函数可理解为具有个参数的随机变量族。
- 随机过程
  - 定义
    - 当随机函数中只有一个自变量，且（一般表示时间或距离）时，称为随机过程，记为。
  - 理解
    - 横向：随机过程是所有实现的集合。
    - 纵向：随机过程是依赖于一个参数的一族随机变量。
- 随机场
  - 定义
    - 当随机函数依赖于多个自变量时，称随机场。
  - 三元随机场的理解
    - 随机场中是依赖于三个参数（空间点的三个直角坐标）的一族随机变量，称为区域化变量。
    - 随机场是其所有实现的集合，每一个实现都是一个三元实值函数或空间点函数。
区域化变量
- 区域化
  - 定义
    - 一个变量呈现为空间分布。
- 区域化变量
  - 定义
    - 以空间点的三个直角坐标为自变量的随机场。
  - 与普通随机变量的不同
    - 普通随机变量的取值按某种概率分布而变化，而区域化变量则根据其在一个域内的位置取不同的值。
    - 即区域化变量是普通随机变量在域内确定位置上的特定取值，它是随机变量与位置有关的随机函数。
- 性质
  - 结构性：区域化变量具有一般的或平均的结构性质，即在空间两个不同点及（为向量）处的数值与具有某种程度的相关性，这种相关性依赖两点间的向量及研究变量特征。
  - 随机性：区域化变量是一个随机场，具有局部的、随机的、异常的性质。当空间一点固定之后，就是一个随机变量。
  - 空间局限性：区域化变量往往只存在于一定的空间范围内，如矿石品位只存在于矿化空间内、群落中某一林分类型的分布。这一空间称为区域化变量的几何域。
  - 不同程度的连续性：不同的区域化变量具有不同程度的连续性，连续性可通过相邻样点之间的变异函数来描述。
  - 不同类型的各向异性：区域化变量如果在各个方向上的性质变化（变异）相同，则称为各向同性若在各个方向上变异不同，则称为各向异性。
相关前置公式及性质
- 数学期望
  - 设为常数，则。
  - 设为随机变量，为常数，则。
  - 设与为随机变量，则。
  - 设与为互相独立的随机变量，则。
- 方差
  - 设为常数，则。
  - 设为随机变量，为常数，则。
  - 设与为随机变量，则。
  - 设与为互相独立的随机变量，则。
- 协方差
  - 设与为常数，则。
  - 设、与为随机变量，则。
协方差函数
- 随机过程的协方差函数
  - 随机过程在时刻处两个随机变量,的二阶混合中心矩成为随机过程的协方差函数，记为或。
- 区域化变量的协方差函数
  - 在空间两点和（为向量）处两个随机变量,的二阶混合中心矩成为随机过程的协方差函数，记为或。
  - 当时，有，称为先验方差函数，记为。
- 实际计算
  - 设区域化变量满足（准）二阶平稳假设，为两样本点空间分隔距离，和分别是在空间位置和上的观测值（），则计算协方差公式如下：
  - 其中与分别表示与的样本平均数。
- 协方差函数性质
  - 时，即
  - 为非负定函数
变异函数
- 定义
  - 在任一方向上，相距的两个区域化变量值和的增量的方差，记为。
- 公式
- 实际计算
  - 设区域化变量满足（准）二阶平稳假设或（准）本征假设，为两样本点空间分隔距离，和分别是在空间位置和上的观测值（），则计算实验变异函数如下：
  - 例题：一研究对象在水平方向上的采样数据（至依次从左往右排布），满足二阶平稳假设或本征假设，采样值如表所示，点间分隔距离，计算。
    - 列出数据对查找表：
    - 计算变异函数值：
- 性质
  - 时，即
  - 为非负定函数
- 功能
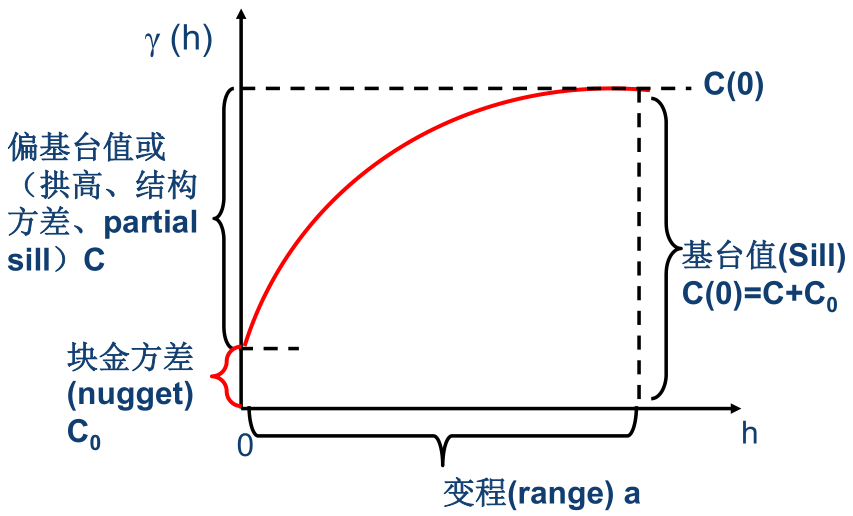
  - 变异函数通过“变程”反映变量的影响范围
    - 通常变异函数为一单调递增函数，当超过某一正值后，变异函数不再继续单调地增大，而往往稳定在一个极限值附近，这种现象称为“跃迁现象”。
    - 此时称为变程，称为基台值。
    - 在二阶平稳假设下，。
    - 变程表示区域化变量从存在空间相关状态（当时）转向不存在空间相关状态（当时）的转折点。
    - 变程的大小反映区域化变量影响范围的大小，或说反映该变量自相关范围的大小。也可说变程是区域化变量空间变异尺度或空间自相关尺度。
    - 基台值的大小反映区域化变量变化幅度的大小，即反映区域化变量在研究范围内变异的强度。
    - 凡具有一个变程和一个基台值的变异函数，称为“跃迁型”的变异函数。
  - 不同方向上的变异函数图可反映区域化变量的各向异性
    - 如果在各个方向上区域化变量的变异性相同或相近，则称区域化变量是各向同性的，反之称为各向异性。
    - 各向同性是相对的，各向异性是绝对的。
  - 块金常数的大小可反映区域化变量的随机性大小
    - 的现象被称为“块金效应”，被称为块金常数或块金方差。
    - 块金常数反应了区域化变量内部随机性的可能程度。
    - 产生原因之一：微观结构，即区域化变量在小于抽样尺度时所具有的变异性，当样点间的距离大于微域结构的范围，或样点样品的大小大于微域结构的范围就会出现块金效应。
    - 产生原因之二：采样、测量和分析等误差。
  - 变异函数在原点处的性状可反映区域化变量的空间连续性
    - 抛物线型
    - 线性型
    - 间断型
    - 随机型
    - 过渡型（实际研究工作中最常遇到）
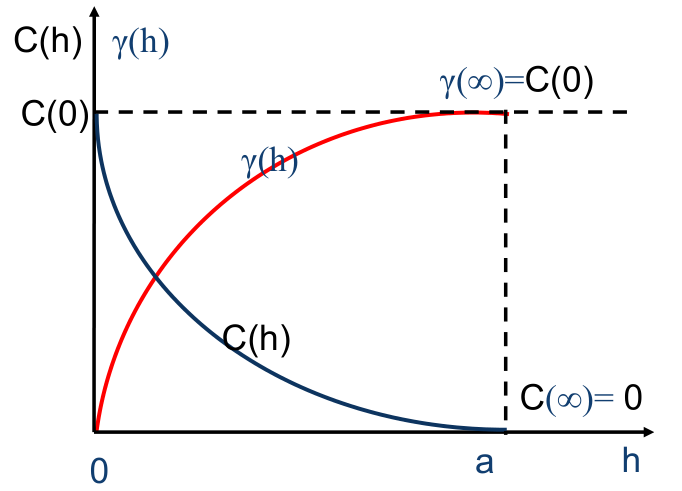
协方差函数与变异函数的关系

地统计学理论假设
- 平稳假设
  - 设某一区域化变量的任意维度分布函数不因空间点发生位移而改变，即对于，都有。
  - 简单来说，即只依赖于，而与无关。
- 二阶平稳假设（弱平稳假设）
  - 条件
    - 整个研究区内的数学期望均存在，且等于常数，即，其中为常数。
    - 整个研究区内的协方差函数存在且平稳，即。
  - 推论
    - 协方差（函数）平稳意味着方差（函数）和变异函数的平稳。
    - 在二阶平稳假设条件下，变异函数、协方差函数和方差函数三者之间有重要的关系，即。
    - 协方差函数和变异函数都表示相距为的两个变量和之间的自相关特性，这时是两个等效的函数。
    - 空间相关函数为。
  - 准二阶平稳假设
    - 区域化变量在有限大小的邻域内满足二阶平稳假设，则称其满足准二阶平稳假设。
- 本征假设（内蕴假设）
  - 条件
    - 整个研究区内，区域化变量的增量的数学期望为，即。若存在，则等价于，其中为常数。
    - 整个研究区内，区域化变量的增量的方差函数存在且平稳，即。
  - 准本征（内蕴）假设
    - 区域化变量在有限大小的邻域内满足本征（内蕴）假设，则称其满足准本征（内蕴）假设。

变异函数结构分析

变异函数的理论模型
- 有基台值模型
  - 纯块金效应模型
    - 公式
    - 参数说明
      - ：块金常数（等于先验方差）
  - 球状模型
    - 公式
    - 参数说明
      - ：块金常数
      - ：拱高（偏基台值、结构方差）
      - ：基台值
      - ：变程
    - 标准球状模型
  - 指数模型
    - 公式
    - 参数说明
      - ：块金常数
      - ：拱高（偏基台值、结构方差）
      - ：基台值
      - ：变程（因为）
    - 标准指数模型
  - 高斯模型
    - 公式
    - 参数说明
      - ：块金常数
      - ：拱高（偏基台值、结构方差）
      - ：基台值
      - ：变程（因为）
    - 标准高斯模型
  - 线性有基台值模型
    - 公式
    - 参数说明
      - ：块金常数
      - ：拱高（偏基台值、结构方差）
      - ：基台值
      - ：变程
      - ：直线斜率（常数）
- 无基台值模型
  - 线性无基台值模型
    - 公式
    - 参数说明
      - ：块金常数
      - ：直线斜率（常数）
  - 幂函数模型
    - 公式
    - 参数说明
      - ：取值范围为的幂指数
      - ：常数
  - 对数模型
    - 公式
    - 参数说明
      - ：常数
- 孔穴效应模型
  - 当变异函数在大于一定的距离后，并非单调递增，而是以一定的周期进行波动，此时变异函数曲线就显示出一种“孔穴效应”。
变异函数的结构分析
- 结构分析
  - 就是构造一个变异函数模型对于全部有效结构信息作定量化的概括，以表征区域化变量的主要特征。
- 结构分析的主要方法
  - 套合结构
- 套合结构
  - 就是把分别出现在不同距离上和（或）不同方向上同时起作用的变异性组合起来，分为单一方向上的套合结构和不同方向上的套合结构。
- 套合结构表达式
  - 套和结构可以表示为多个变异函数之和，每一个变异函数代表一种特定尺度上的变异性，即。
  - 例子
    - 设区域化变量在某一方向上的变异性是由、和组成：
    - 微观尺度为纯块金效应模型：
    - 变程为的球状模型：
    - 变程为（）的球状模型：
    - 则套合结构：
变异函数理论模型的最优拟合
- 定义
  - 根据变异函数的计算值，选择合适的理论模型来拟合一条最优的理论变异函数曲线，通常称为最优拟合。
- 分类
  - 人工拟合
  - 自动拟合
    - 最小二乘法
    - 加权回归法
结构分析的基本步骤
- 区域化变量选择
  - 根据研究目的而定
  - 要有明确物理意义
  - 最好能定量表示
- 数据的审议
  - 空间取样设计：方式、样点间距离大小、样本数量的大小、采样密度、取样方法
  - 数据代表性：采样均匀性、时空一致性等
- 数据的统计分析
  - 基本分析：平均值、方差、标准差、变异系数等
  - 相关分析：协同克里金法
  - 异常值识别及处理：全局和局部离群值
  - 分布检验及数据转换
- 变异函数的计算
  - 等间距的规则网格数据
    - 全部采样
    - 随机采样
  - 非等间距的不规则网格数据
    - 分组采样
      - 角度分组：与角度在范围内的归为一组
      - 距离分组：与相距归为一组
    - 具体实现
      - 扇区分组
        
        步长（）
        
        太大会掩盖区域化变量的局部微观结构。
        
        太小会产生很多空步长组或组内样点对很少。
        
        一般满足步长乘以步长组数等于样点间最大距离的一半。
        
        角度容限值（）
        
        太大会包含其他方向上的变异。
        
        太小会造成组数增加，计算量增加，某些组内的样点对可能过少，变异函数可靠性差。
      - 格网分组
        
        格网分组后的表面成为变异函数表面。
        
        表面中每一个栅格为一个组。
        
        颜色代表变异函数的大小。
        
        图案关于中心对称。
- 变异函数的结构分析——各向异性
  - 结构分析的目的在于通过分析各种实验变异函数来分析所研究的区域化现象的主要结构特征。
- 理论变异函数模型的最优拟合及检验
- 变异函数理论模型的专业分析

克里金法

估计方差
- 概念
  - 若某一区域化变量在某一点处的实际值为，其估计值为，则估计误差为。
  - 若该区域化变量满足二阶平稳假设，则估计误差也满足二阶平稳假设，估计误差的数学期望为（为常数），估计方差（估计误差的方差）为。
- 估计量评价
  - 无偏性：
  - 最优性：
- 线性估计量（线性平稳地统计学）
  - 假设要根据位于点（）的个样品值来估计中心点在、体积为的块段的平均值为, 显然估计量是诸的函数。
  - 通常采用线性函数，即，其中为每个样品点的权重。
  - 无偏性条件为。
  - 上述无偏性条件下的估计方差为。
克里金法概述
- 定义
  - 又称空间局部估计或空间局部插值法，是建立在变异函数理论及结构分析基础上，在有限区域内对区域化变量的取值进行线性无偏最优估计的一种方法。
- 种类
  - 线性平稳地统计学范畴
    - 简单克里金法
    - 普通克里金法
  - 线性非平稳地统计学范畴
    - 泛克里金法
  - 非线性地统计学范畴
    - 对数正态克里金法
    - 指示克里金法
    - 概率克里金法
    - 析取克里金法
  - 多元地统计学范畴
    - 协同克里金法
- 估计量
  - 表达式
  - 参数说明
    - ：研究区域内任一点的位置
    - ：权重系数
  - 条件
    - 无偏性：
    - 最优性：
- 估值过程
  - 数据检查
  - 模型拟合
  - 模型诊断
  - 模型比较
简单克里金法
- 假设
  - 区域化变量满足二阶平稳假设
  - 区域化变量数学期望为已知的常数
  - 协方差函数和变异函数存在且平稳
- 变形：
- 估计量：
- 方程组
- 参数求解矩阵
- 估计方差：
- 估计值求算：
- 例题：已知个点（编号为至）的坐标与高程（均值为已知常数）和待估点（编号为）的坐标，用简单克里金法插值高程。
  - 参数求解矩阵
  - 估计值求算：
  - 估计方差：
普通克里金法
- 假设
  - 区域化变量满足二阶平稳假设
  - 区域化变量数学期望为未知的常数
  - 协方差函数和变异函数存在且平稳
- 估计量：
- 方程组
- 协方差函数形式
  - 参数求解矩阵：
  - 估计方差：
- 变异函数形式
  - 参数求解矩阵：
  - 估计方差：
- 估计值求算：
- 例题：已知个点（编号为至）的坐标与高程（均值为未知常数）和待估点（编号为）的坐标，用简单克里金法插值高程。
  - 参数求解矩阵
  - 估计值求算：
  - 估计方差：
- 块段估计
  - 点采样数据：将块段离散成若干点，求采样点和各离散点之间的协方差函数或变异函数值之和，后取平均值（除以块段离散成的点数）。
  - 块段采样数据：将采样和待估块段都离散成若干点，求各采样块段离散点和各待估块段离散点之间的协方差函数或变异函数值之和，后取平均值（除以两块段离散成的点数之积）。
克里金法的内涵
- 基于采样数据反映的区域化变量的结构信息（变异函数或协方差函数提供），根据待估点或块段有限邻域内的采样点数据，考虑样本点的空间相互位置关系（矩阵）、与待估点的空间位置关系（矩阵），对待估点进行的一种线性无偏最优估计，并且能给出估计精度，比其他传统方法更精确、更符合实际。
克里金法的几点说明
- 总体特征
  - 克里金矩阵和估计构形：数据构形相同，矩阵就相同。
  - 表达式通用性：不论采样数据和待估数据为点或块段，不论协方差函数和变异函数表征为何种结构模型，克里金方程组和克里金估计方差完全通用。
  - 估计可靠性。
  - 若已知协方差函数或变异函数，则可提前计算克里金估计方差，用于指导采样设计。
- 权重系数特点
  - 可减弱丛聚效应：在克里金估计中，不会由于一些样点丛聚在一起而增大其权重系数（假设各向同性）。
  - 屏蔽效应：相近方向上的两点，距离近的一点的权重远大于远的一点的权重。屏蔽效应与块金常数有很大的关系。
  - 权重可正可负性：可获取大于最大或小于最小的样本值的插值结果。
  - 块金值的大小对权重影响：增加块金值会使插值过程更接近于简单算术平均。极端情形——纯块金效应模型，样本权重相同，结果为样本的算术平均。
- 理论模型对克里金估计的影响
  - 偏基台值
    - 越大：变异越强，距离近的权重就越大，估计难度也越大，估计方差越大。
    - 越小：变异越弱，距离近的权重就越小，估计难度也越小，估计方差越小。
  - 变程
    - 越大：变异越平缓，距离近的权重就越小，估计难度越小，估计方差越小。
    - 越小：变异越剧烈，距离近的权重就越大，估计难度越大，估计方差越大。
  - 块金值
    - 越大：屏蔽效应减弱，距离近的权重就越小，同时样点间相关性也越小，估计难度越大，估计方差越大。
    - 越小：屏蔽效应增强，距离近的权重就越大，同时样点间相关性也越大，估计难度越小，估计方差越小。
泛克里金法
- 漂移
  - 定义
    - 非平稳区域化变量的数学期望，在任一点上的漂移就是该点上区域化变量的数学期望。形式化表达为。
  - 用邻域模型的研究
    - 在给定的以点为中心的邻域内的任一点其漂移可用如下函数表示：
    - 其中为已知函数（常为多项式），为未知系数。
    - 实际工作中，根据中心点有限邻域内的全部有效数据计算该邻域的漂移，一般只需要一次或二次多项式。
- 涨落
  - 对于有漂移的区域化变量，假设可分解为漂移和涨落两部分，形式化表示为。其中为该点处的漂移，为涨落。
  - 上述分解可以理解为：是由两个不同尺度的现象合成的，是在较大尺度下可以观察到的现象变化，是在较小尺度下的现象变化。
  - 涨落的数学期望为。

空间确定性插值

探索性数据分析
- 检查数据分布
  - 目的：探查数据、分析数据的特征
  - 工具
    - 直方图
    - QQPlot图
      - Box-Cox变换：
      - log变换：
      - 反正弦变换：
- 寻找全局和局部离群值
  - 全局离群值：对于数据集中所有点的值，具有很高或很低值的观测样点。
  - 局部离群值：在数据集中，对于其周围点的值具有很高或很低值的观测样点。
  - 工具
    - 直方图
    - 半变异/协方差函数云图
      - 半变异函数云图：
      - 协方差函数云图：
    - Vonoroi图
      - 生成方法：多边形内任何位置到这一样点的距离都比该多边形到其他样点的距离要近。
- 全局趋势分析
  - 目的：地统计分析时，为满足平稳假设，要剔除全局趋势。剔除后，可模拟随机短期变异。为合理预测，之后必须将全局趋势再还原回去。
  - 工具
    - Trend Analysis工具
- 检测空间自相关及方向变异
  - 工具
    - 半变异/协方差函数云图
空间确定性插值
- 插值定义
  - 空间插值：将离散的数据点转化为连续的数据曲面。
  - 内插：在已观测点的区域内估算未观测点的数据的过程。
  - 外推：在已观测点的区域外估算未观测点的数据的过程。
- 插值法分类（加粗者包含克里金法）
  - 根据已知插值数据的不同
    - 点插值法
    - 面（区域）插值法
  - 根据插值时采用的数据点数不同
    - 全局（整体）插值法
    - 局部插值法
  - 根据插值方法是否提供预测的误差评价
    - 确定性插值法（不提供）
    - 统计插值法（提供）
  - 根据插值后表面是否通过采样点
    - 精确插值法
    - 非精确（近似）插值法
- 径向基函数插值法
  - 概念
    - 径向基函数插值法是一系列精确插值方法的统称。
  - 条件
    - 生成的表面经过每个采样点
    - 表面有最小的曲率
- 交叉验证
  - 首先从采样数据集中删除一点，然后使用其它采样值点估计此删除点的值，最后计算此点实测值和估计值的差，重复以上步骤直到遍历所有采样点。
  - 均方根预测误差：
  - 标准化均方根预测误差：
- 验证
  - 将采样数据集分成两个子集：一个称为训练数据集，用于趋势分析及预插值；一个称为检验数据集，用于插值精度检测。
  - 若检验效果好，则将全部数据用于插值预测。

软件操作

简单克里金法
- 数据集设置：[Dataset]中可以设置源数据集和需要插值的字段。
- 克里金法及数据趋势参数设置：左侧[Kriging Type]选择[Simple]，[Output Surface Type]选[Prediction]；右侧[Dataset #1]中[Transformation Type]选择一个合适的数据变形，[Order of trend removal]按照ESDA的趋势分析选择合适的多项式拟合阶数。
- 全局趋势函数类型及参数设置：右侧[General Properties]中[Kernel Function]可以设置对变量空间趋势拟合的函数类型。
- 半变异/协方差函数建模：右侧[General]中[Variable]可以选择显示半变异函数或协方差函数的表面，[Model Nugget]中可以设置块金效应的建模参数，[Model #1]中可以选择区域化变量的理论模型（如球状模型[Spherical]并开启各向异性[Anisotropy]）。
- 搜索邻域范围设置：右侧[Search Neighborhood]可以设置搜索邻域的相关参数。
- 预测结果的交叉验证：观察[Regression function]上方的回归直线方程（深色）是否与1:1线（浅色）吻合情况。
- 生成简单克里金预测表面图
普通克里金法
- 数据集设置
- 克里金法及数据趋势参数设置：左侧[Kriging Type]选择[Ordinary]；其余与简单克里金类似。
- 全局趋势函数类型及参数设置
- 半变异/协方差函数建模
- 搜索邻域范围设置
- 预测结果的交叉验证
- 生成普通克里金预测表面图
指示克里金法
- 数据集设置
- 克里金法及数据趋势参数设置：左侧[Kriging Type]选择[Indicator]，[Output Surface Type]按需求选择[Probability]或者[Standard Error of Indicators]；右侧[Dataset #1]中两者都设置为[None]（指示克里金法无需假设数据来自正态分布）；右侧[Primary Threshold]中可以设置主阈值相关参数；右侧[Cutoffs]改变[Number of Cutoffs]值可以设置多个阈值。
- 半变异/协方差函数建模
- 搜索邻域范围设置
- 预测结果的交叉验证
- 生成指示克里金概率表面图
外推
- 双击生成的预测表面图层，切换至[Extent]选项卡，将[Set the extent to]改为[the rectanglar extent of provin_srtm]，其中[provin_srtm]为边界面要素图层。
假裁切
- 双击[Layers]，切换至[Data Frame]选项卡，[Clip Option]中选择[Clip to shape]，点击[Specify Shape]按钮。
- 在弹出的对话框中选择[Outline of feature]，[Layer]选[provin_srtm]，其中[provin_srtm]为边界面要素图层。
真裁切
- 右击克里金预测表面图层，选择[Data]下的[Export to Raster]，选择一个无中文的路径保存栅格数据。
- 打开[ArcToolbox]中[Spatial Analyst Tools]下[Extraction]下的[Extract by Mask]。
- 在弹出的对话框中，[Input raster]选择上述保存的栅格文件，[Input raster or feature mask data]选[provin_srtm]（[provin_srtm]为边界面要素图层），[Output raster]选择保存的路径。
训练/检验数据集生成及使用
- 打开[Geostatistical Analyst]菜单下的[Subset Features]。
- 在弹出的对话框中，[Input feature]选待插值的点要素图层，[Output training feature class]选择训练数据集的保存路径，[Output test feature class]选择检验数据集的保存路径，[Size of training feature subset]输入90。
- 对生成的训练数据集点要素图层进行克里金插值。
- 在上述生成的表面图层上右击，选择[Validation/Prediction]。
- 在弹出的对话框中，[Input point observation locations]选上述生成的检验数据集点要素图层，[Field to validate on]选择上述插值的字段，[Output statistics at point locations]选择保存结果的文件路径。
- 右击新生成的点要素图层，选择[Open Attribute Table]，滚动至最右侧即可查看检验结果。
Excel操作
- $纬度（度）$ 位于E2:E677， $海拔高度$ 位于F2:F677， $温度$ 位于G2:G677。
- 相关系数：CORREL(array1, array2)
  - $海拔温度$ ：=CORREL(F:F,G:G)
  - $纬度温度$ ：=CORREL(E:E,G:G)
- 检验（双尾反函数）：T.INV.2T(probability, deg_freedom)
  - ：=T.INV.2T(0.01,676-2)
- 一元线性回归截距：INTERCEPT(known_y's, known_x's)
  - 温度与海拔的回归方程参数：=INTERCEPT(G:G,F:F)
- 一元线性回归斜率：SLOPE(known_y's, known_x's)
  - 温度与海拔的回归方程参数：=SLOPE(G:G,F:F)
- 多元线性回归：LINEST(known_y's, [known_x's], [const], [stats])
  - 备注：该数组函数需要一个的空间，其中为自变量个数。
  - 温度与维度、海拔的回归系数：=LINEST(G2:G677,E2:F677,TRUE,TRUE)
- 矩阵求逆：MINVERSE(array)
- 矩阵相乘：MMULT(array1, array2)
- 矩阵转置：TRANSPOSE(array)

概论

地统计学概念

地统计学基础

频数分布

统计特征数

相关分析

回归分析

区域化变量理论

随机场

协方差函数

变异函数

协方差函数与变异函数的关系

地统计学理论假设

变异函数结构分析

变异函数的理论模型

变异函数的结构分析

结构分析的基本步骤

克里金法

估计方差

克里金法概述

简单克里金法

普通克里金法

克里金法的内涵

克里金法的几点说明

泛克里金法

空间确定性插值

探索性数据分析

空间确定性插值

软件操作

简单克里金法

普通克里金法

指示克里金法

外推

假裁切

真裁切

训练/检验数据集生成及使用

Excel操作