A - Odd Palindrome

原题面

描述

We say that a string is odd if and only if all palindromic substrings of the string have odd length.
Given a string s, determine if it is odd or not.
A substring of a string s is a nonempty sequence of consecutive characters from s. A palindromic substring is a substring that reads the same forwards and backwards.

输入

The input consists of a single line containing the string s ().
It is guaranteed that s consists of lowercase ASCII letters (‘a’–‘z’) only.

输出

If s is odd, then print “Odd.” on a single line (without quotation marks). Otherwise, print “Or not.” on a single line (without quotation marks).

时空限制

时间限制：
空间限制：

样例

输入	输出
amanaplanacanalpanama	Odd.
madamimadam	Odd.
annamyfriend	Or not.
nopalindromes	Odd.

题解

题意

给定字符串s，判断s中所有回文子串长度是否都为奇数。

思路

暴力枚举s的所有子串，并判断其是否为回文字符串以及其长度是否为奇数。

时间复杂度

代码

def palindromic(s: str) -> bool:
    l = len(s)
    for i in range(l):
        if s[i] != s[l - i - 1]:
            return False
    return True

def check(s: str) -> bool:
    for i in range(len(s) - 1):        # [0, len(s) - 2]
        for j in range(i + 1, len(s)): # [i + 1, len(s) - 1]
            if palindromic(s[i : j + 1]) and (j - i + 1) % 2 == 0:
                return False
    return True

while True:
    s = input()
    if s == "":
        break
    print("Odd." if check(s) else "Or not.")

E. Straight Shot

原题面

描述

You have a toy robot that walks straight at a constant speed , and you wish for it to travel on the two-dimensional plane from to . If the plane were empty, you could start the robot facing straight east from the origin, and it would walk there in time. Unfortunately, between the start and the destination are n moving sidewalks, each moving directly north or south, which affect the robot’s position while it is walking.
The direction that robot is facing is not changed by the sidewalks; the robot will face in the same orientation for the entire duration of its walk. These sidewalks are aligned with the 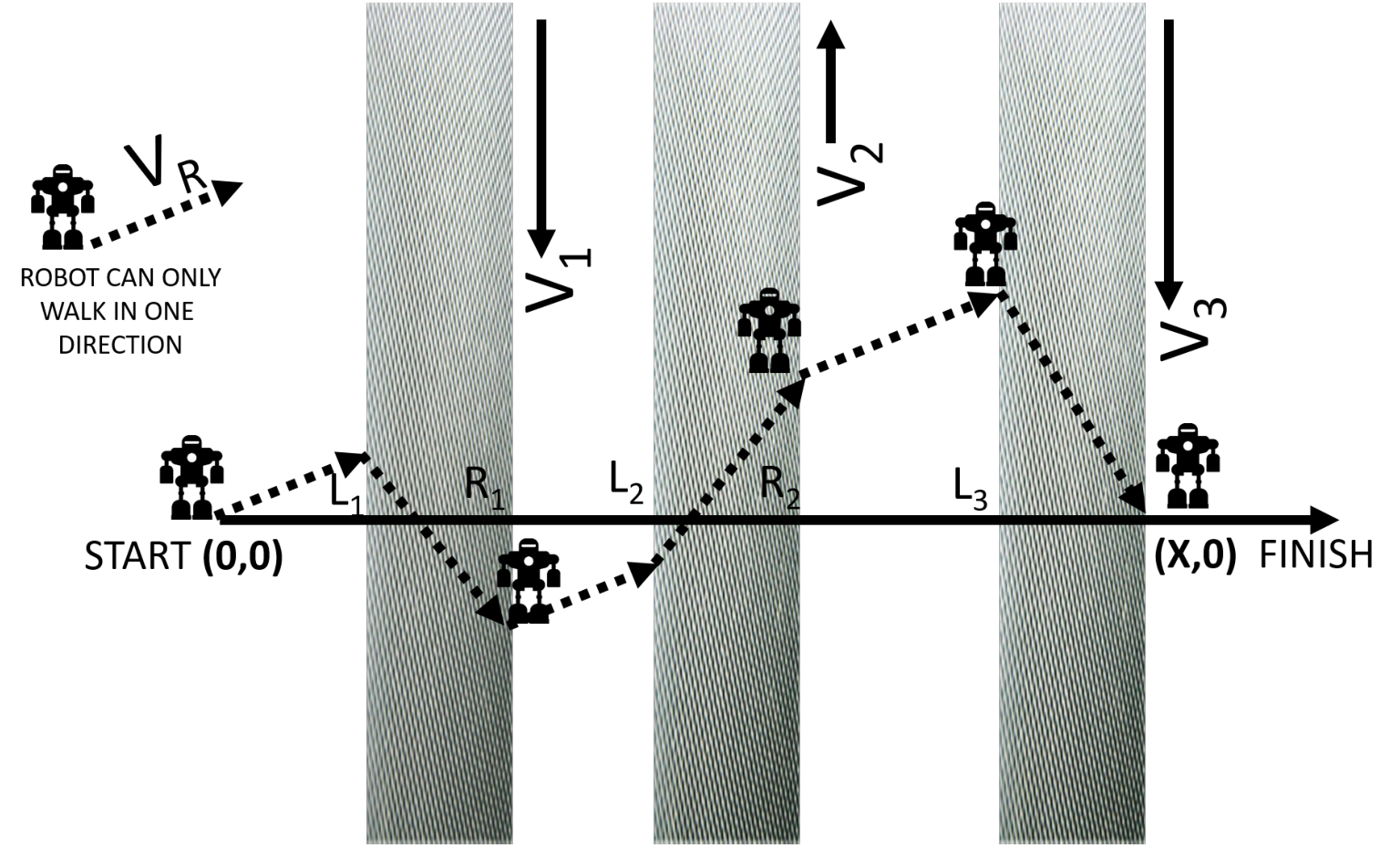-axis and are infinitely long. You still must get the robot to go from start to finish, but you’ll need to adjust the orientation of the robot at the start. Given that you choose this direction correctly, so that the robot arrives exactly at the destination, how long will it take the robot to get there?

One final caveat: You don’t want the toy robot to walk for too long. If the robot cannot reach the destination in at most twice the time it would take in the absence of all moving sidewalks (i.e., ), indicate this.

输入

The first line consists of three space-separated numbers , , and (; ; ). Note that is not necessarily an integer.
Each of the next lines contains three space-separated numbers , , and (; ), describing the th moving sidewalk. The integer denotes the left edge of the sidewalk, the integer denotes the right edge of the sidewalk, and the decimal number denotes the speed of the sidewalk. A positive speed means the sidewalk moves north, while a negative speed means the sidewalk moves south.

输出

If the robot cannot reach the destination in at most twice the time it would take in the absence of all moving sidewalks, output “Too hard” on a single line (without quotation marks).
Otherwise, output, on a single line, the travel time of the robot from the start to the destination, rounded and displayed to exactly three decimal places.

时空限制

时间限制：
空间限制：

样例

输入	输出
1 806873 66 91411 631975 -57.5	15055.988
2 422193 100 38180 307590 86.4 366035 403677 -4.7	5043.896
1 670764 22.4 113447 642610 -64.8	Too hard

题解

题意

求一质点从恰好运动到的时间。
在起点处可设定其速度的方位角（从轴正方向起顺时针转过的角度，其中），之后不可再改变该角度。
在质点向运动的过程中，若质点当前坐标满足，则会叠加上平行于轴的速度矢量（以轴正方向为的正方向）。
质点全程分段做匀速直线运动。

思路

将初速度正交分解到平行于坐标轴方向，以坐标轴的正方向为分速度的正方向，分别为方向上的速度与方向上的速度。
当质点位于传送带（sidewalk）上时，方向上的速度改变为。
由于要求恰好运动到，则需要保证方向上的位移为。
质点位于第个传送带上时，通过该传送带（横坐标不在该传送带区间内）的时间只与方向上的速度有关，为。
在上述的时间内方向上的位移为。
该部分位移累计。
令、，则。
注意到常数实际表示所有传送带的总长度，故不在传送带上的总长度为，通过时间为。
在上述的时间内方向上的位移为。
故方向上的总位移为。
令，由于，则，。
若，则可计算时间。

时间复杂度

代码

from math import sqrt

n, x, vr = [float(_) for _ in input().split()]
n = int(n)
C = 0.0
for i in range(n):
    l, r, vs = [float(_) for _ in input().split()]
    C += (r - l) * vs / vr
try:
    sin = 1.0 if n == 0 else sqrt(1.0 - C ** 2 / x ** 2)
    t = x / (vr * sin)
    print("Too hard" if vr * t > 2.0 * x else "%.3lf" % t)
except:
    print("Too hard")

L - Delayed Work

原题面

描述

You own a company that hires painters to paint houses. You can hire as many painters as you want, but for every painter you hire, you have to pay dollars (independent of how long the painter works on the house). In addition, you have to pay a penalty of dollars overall if it takes days to finish painting the house. This penalty does not depend on the number of painters you hire; furthermore, even if the time taken is not a whole number of days, you are only penalized for the exact time taken.
All painters paint at the same rate. One painter can finish painting the house in days. The painters cooperate so well that it will only take days for painters to finish painting the house.
What is the minimum amount of money you will have to pay, including what you pay to the painters and the cost penalty, to get a house painted?

输入

The input consists of a single line containing three space-separated integers , , and ().

输出

Print, on a single line, the minimum cost to have the house painted, rounded and displayed to exactly three decimal places.

时空限制

时间限制：
空间限制：

样例

输入	输出
31 41 59	549.200
3 4 5	16.000

题解

题意

雇个工人花费天完成一个总量为的工程，其中。整个工期内需要支付每个工人费用；另外，工期结束后还需支付费用。求最小花费。

思路

目标函数为，其中为正整数。
根据基本不等式，得（当且仅当，即时取等号）。
最小花费则为与 $f\left(\left\lfloor\dfrac{KP}X\right\rfloor+1\right)$ 中的较小者。

时间复杂度

代码

from math import sqrt

k, p, x = [int(x) for x in input().split()]
m = int(sqrt(k * p / x))
f = lambda m: m * x + p * k / m
print("%.3lf" % min(f(m), f(m + 1)))

O - Halfway

原题面

描述

A friend of yours has written a program that compares every pair of a list of items. With n items, it works as follows. First, it prints a 1, and it compares item to items . It then prints a 2, and compares item to items . It continues like that until every pair of items has been compared exactly once. If it compares item to item , it will not later compare item to item . Also, it does not compare any item to itself.
Your friend wants to know when his program is halfway done. For a program that makes an odd number of total comparisons, this is when it is doing the middle comparison. For a program that makes an even number of total comparisons, this is when it is doing the first of the two middle comparisons.
What will the last number printed be when the program is halfway done?
Note that since the earlier items have more comparisons than the later items, the answer is not
simply .

输入

The input consists of a single line containing the integer ().

输出

Print, on a single line, the last number your friend’s program prints when it is halfway done.

时空限制

时间限制：
空间限制：

样例

输入	输出
4	1

题解

题意

输出下列C++程序的最后一个输出的值。

#include <cstdio>
long long n;
void work() {
    long long cnt = 0;
    long long tot = n * (n - 1) / 2;
    long long half = (tot + 1) / 2;
    for (int i = 1; i < n; ++i) {
        printf("%d\n", i);
        for (int j = i + 1; j <= n; ++j) {
            ++cnt;
            if (cnt == half)
                return;
        }
    }
}
int main() {
    scanf("%lld", &n);
    work();
    return 0;
}

思路

比较总次数；中间次比较次数。
当外层循环执行第次时，内层循环最多会将cnt的值加上。
问题可转化为求满足的最小正整数。
变形得。
二次函数的对称轴为直线，故答案在区间上单调递减。因此可以使用二分答案法进行求解。
由于当取，即外层循环执行到第次时，内层循环并不会改变cnt的值，因此答案不会为。

时间复杂度

代码

n = int(input())
C = (n * (n - 1) // 2 + 1) // 2
l, r = 1, n - 1
ans = 1
f = lambda x: x ** 2 - (2 * n - 1) * x + 2 * C
while l <= r:
    mid = l + r >> 1
    if f(mid) <= 0:
        ans = mid
        r = mid - 1
    else:
        l = mid + 1
print(ans)

Q - Unloaded Die

原题面

描述

Consider a six-sided die, with sides labeled through . We say the die is fair if each of its sides is equally likely to be face up after a roll. We say the die is loaded if it isn’t fair. For example, if the side marked is twice as likely to come up as than any other side, we are dealing with a loaded
die.
For any die, define the expected result of rolling the die to be equal to the average of the values of the sides, weighted by the probability of those sides coming up. For example, all six sides of a fair die are equally likely to come up, and thus the expected result of rolling it is .
You are given a loaded die, and you would like to unload it to make it more closely resemble a fair die. To do so, you can erase the number on one of the sides, and replace it with a new number which does not need to be an integer or even positive. You want to do so in such a way that

The expected result of rolling the die is , just like a fair die.
The difference between the old label and the new label on the side you change is as small as possible.

输入

The input consists of a single line containing six space-separated nonnegative real numbers , where represents the probability that side (currently labeled by the number ) is rolled.
It is guaranteed that the given numbers will sum to .

输出

Print, on a single line, the absolute value of the difference between the new label and old label, rounded and displayed to exactly three decimal places.

时空限制

时间限制：
空间限制：

样例

输入	输出
0.16666 0.16667 0.16667 0.16666 0.16667 0.16667	0.000
0.2 0.2 0.1 0.2 0.2 0.1	1.000

题解

题意

给出一个六面骰子（点数为至）每个面朝上的概率，修改至多一个面的点数，使期望为，求最小的修改差值。

思路

未修改前的期望为。
设被修改的面原点数为，修改后点数为。
修改后的期望为。
修改差值为。
为使差值最小，取最大的即可。

时间复杂度

代码

v = [float(x) for x in input().split()]
e = 0.0
for i in range(6):
    e += (i + 1) * v[i]
v.sort()
print("%.3lf" % (abs(e - 3.5) / max(v)))

R - Star Arrangements

原题面

描述

The recent vote in Puerto Rico favoring United States statehood has made flag makers very excited. An updated flag with stars rather than the current one with would cause a huge jump in U.S. flag sales. The current pattern for stars is five rows of stars, interlaced with four offset rows of stars. The rows alternate until all stars are represented.

* * * * * *
 * * * * *
* * * * * *
 * * * * *
* * * * * *
 * * * * *
* * * * * *
 * * * * *
* * * * * *

This pattern has the property that adjacent rows differ by no more than one star. We represent this star arrangement compactly by the number of stars in the first two rows: 6,5.
A

-star flag that has the same property can have three rows of

stars, interlaced with three rows of

stars (with a compact representation of 9,8). Conversely, if a state were to leave the union, one appealing representation would be seven rows of seven stars (7,7).
A flag pattern is visually appealing if it satisfies the following conditions:

Every other row has the same number of stars.
Adjacent rows differ by no more than one star.
The first row cannot have fewer stars than the second row.

Your team sees beyond the short-term change to for the U.S. flag. You want to corner the market on flags for any union of three or more states. Given the number of stars to draw on a flag, find all possible visually appealing flag patterns.

输入

The input consists of a single line containing the integer ().

输出

On the first line, print , followed by a colon. Then, for each visually appealing flag of stars, print its compact representation, one per line.
This list of compact representations should be printed in increasing order of the number of stars in the first row; if there are ties, print them in order of the number of stars in the second row. The cases -by- and -by- are trivial, so do not print those arrangements.
The compact representations must be printed in the form “x,y”, with exactly one comma between x and y and no other characters.

时空限制

时间限制：
空间限制：

样例

输入	输出
3	3: 2,1
50	50: 2,1 2,2 3,2 5,4 5,5 6,5 10,10 13,12 17,16 25,25
51	51: 2,1 3,3 9,8 17,17 26,25

题解

题意

将总共个星号按一行个、一行个的格式交叉排列，其中。求所有排列情况。

思路

分以下三种情况讨论：
一行个、一行个为一组，总共组。
一行个、一行个为一组，总共组，最后多出一行个。
一行个为一组，总共组。
注意且。

时间复杂度

代码

s = int(input())
print("{}:".format(s))
for i in range(2, (s + 1) // 2 + 1):
    if s % (2 * i - 1) == 0 or (s - i) % (2 * i - 1) == 0:
        print("{},{}".format(i, i - 1))
    if s % i == 0:
        print("{},{}".format(i, i))

S - Forbidden Zero

原题面

描述

You’re writing the positive integers in increasing order starting from one. But you’ve never learned the digit zero, and thus omit any number that contains a zero in any position. The first ten integers you write are: and .
You have just written down the integer (which is guaranteed to not contain the digit zero). What will be the next integer that you write down?

输入

The input consists of a single line containing the integer (n$ does not contain the digit zero.

输出

Print, on a single line, the next integer you will be writing down.

时空限制

时间限制：
空间限制：

样例

输入	输出
99	111
1234	1235

题解

题意

求大于的不包含数字的最小正整数。

思路

枚举大于的正整数，判断是否包含数字即可。

时间复杂度

代码

def hasZero(x: int) -> bool:
    while x:
        if x % 10 == 0:
            return True
        x //= 10
    return False

n = int(input())
n += 1
while hasZero(n):
    n += 1
print(n)